小中研究室

勝敗確率計算機(Jリーグバージョン) (Win probability calculator for J League)

Tweet
サッカーにおける得点はポアソン分布に従うことが知られています(詳しく知りたい方はページ下部の「解説」をお読みください)．ここでは両チームの平均得失点，ホーム/アウェー，現在の得失点差，および残り時間を定めると，その試合での試合終了時点での得失点差の確率分布，および勝敗確率を計算して表示するシミュレーションを行います．「1点ビハインドでハーフタイムに入った．逆転の可能性はどれくらい？」などの疑問に，統計と数学でお答えします．
皆様のサッカーライフの一助となれば幸いです．

平均得失点

試合状況

残り時間 (Remaining minutes)：90

得失点差 (Goal difference)：0

予測結果

ホームチーム予測得点(/90分)： 1.8784
アウェーチーム予測得点(/90分)： 1.7378

得失点差の確率関数

勝ち・引き分け・負けの確率

ホームチーム予測勝率： 0.4189
ホームチーム予測分率： 0.2196
ホームチーム予測負率： 0.3615

解説：サッカーとポアソン分布

サッカーは得点の少ないスポーツです．その一方，得点が決まる最小単位の時間，10秒くらいを考えればよいでしょうか，に対して試合時間は90分と非常に長いです．すると，サッカーでの得点は，「挑戦回数が多いものの成功回数が少ないできごと」と解釈できます．
確率の分野では古くから(少なくとも100年以上前から)このようなできごとの特徴を明らかにしようという試みがなされており，今日では「ポアソン分布」として知られるようになっています．まぁ名前はどうでもよくて，「成功確率が小さいできごとに対してたくさん挑戦したときの，最終的な成功回数」が計算できればそれでよいのです．
プロサッカーの場合，1試合1チーム当たりの平均得点は1.30(2017年J1)くらいで，試合時間の最小単位を10秒とすると，成功確率が0.0024のできごとに対して540回(=90*60/10)挑戦したときの成功回数が得点となります．成否は確率的なので，成功回数(つまり，得点)も確率的にばらつくことになります．実際の試合数の割合（2017年J1のデータ）と，ポアソン分布と仮定して算出された割合を並べると(下図)，ポアソン分布が現実を非常によく説明できていることがわかります．

以下の質問について考えてみましょう．

• 1試合平均で1.5得点できるクラブが試合をしていて，残り時間が30分だったとします．残り時間で期待できる得点は何点でしょうか？
• 1試合平均で1.5得点できるクラブAが，これまた1試合平均で1.5失点するクラブBと対戦した時に期待できる得点は何点でしょうか？

これらがわかれば，現在の試合の状況(得失点差，残り時間，対戦クラブ間の実力の関係)から最終的な勝敗の確率を予測できそうです．
前者から考えましょう．こちらは単純のために，「得点と時間が比例する」と仮定するしか無いと思います(実際は終盤のほうが得点は多い傾向にありますが)．従って， 1試合平均で1.5得点できるクラブが試合をしていて，残り時間が30分だったとすると，残り時間では1.5x30/90=0.5点が期待できる得点です．
後者はちょっと込み入っています．前述のとおり，プロサッカーでは1試合の平均得点は1.30(2017年J1)くらいです．従って，平均得点1.5点は攻撃が良いクラブですし，平均失点1.5は守備が若干悪いクラブです．従って，クラブAの期待得点は1.5よりも大きいはずです．
これには統計の力を借ります．2016年から2020年のJリーグ(J1からJ3,5244試合)について，各シーズン各クラブの平均得失点を計算します．そして，「クラブAとクラブBの対戦でのクラブAの得点は，クラブAの平均得点(≒攻撃力)とクラブBの平均失点(≒守備力)に依存する」という仮説を立てます．
この仮説の元，実際の得点との誤差が小さくなる関数を見つけます．結果の図がこちらです．

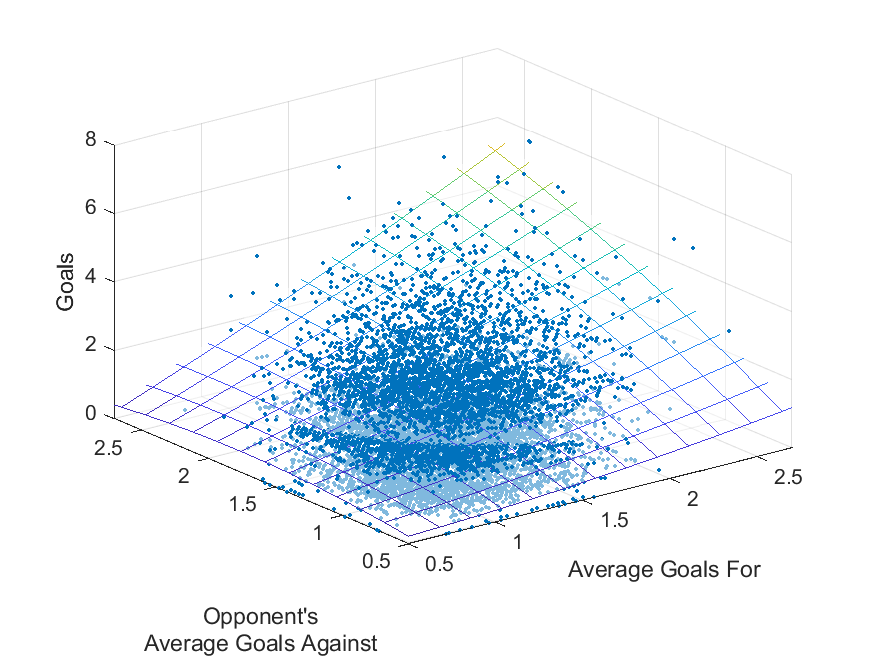
底面の二つの軸がそれぞれのクラブの平均得失点，青い点がゴール数(1試合で2つ点が対応)です．ゴール数の平均の近くを通るように選ばれたのが色の格子で表されている曲面です．ちょっと煩雑になりますが，式を書いてみます．$x_1$がチームAの平均得点，$x_2$ がチームBの平均失点，$y$ がチームAとBが対戦した時のチームAの期待得点です．チームAがホームチームの場合は$x_1$ に$0.1405$(2016年から2020年Jリーグでのホームアドバンテージ)を加えます．

$ y= 0.001057 -0.35439x_1 +0.45372x_2+0.11467 x_1^2 + 0.83828x_1x_2 -0.24727 x_2^2$

この式を利用すると，「1試合平均で1.5得点できるクラブAが，これまた1試合平均で1.5失点するクラブBと対戦した時に期待できる得点」はホーム1.8784点，アウェー1.7378と算出されます．
ここまでの準備で両チームの期待得点が算出できました．あとは残り時間を考慮してそのあとの得点分布を作成し，現在の得失点差を反映させて勝ち・引き分け・負けの確率を合計します．この処理を行うアプリが上に示したものです．

文責：小中英嗣(名城大学理工学部情報工学科)．2021年3月．